Hello mathematicians, puzzlers, and other curious people!
Last time we worked with the formula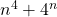 
, we found out its output is sometimes composite (such as when n=4), and sometimes prime (such as when n=1). We’d like to come up with a rule for predicting without evaluating, though, because if I’m curious about whether 
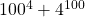is prime, multiplying 100 by itself four times isn’t so bad, but multiplying four by itself 100 times would be unreasonable — try it if you need to convince yourself.
, we found out its output is sometimes composite (such as when n=4), and sometimes prime (such as when n=1). We’d like to come up with a rule for predicting without evaluating, though, because if I’m curious about whether is prime, multiplying 100 by itself four times isn’t so bad, but multiplying four by itself 100 times would be unreasonable — try it if you need to convince yourself.
Your first thought might be “offload the arithmetic to a calculator,” which is a very lazy like a mathematician idea (remember, that’s a good kind of lazy, where we take reliable shortcuts). However, my calculator informs me that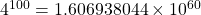 
. Since that’s a higher power of 10 than the number of decimal places it showed me, I’m concerned that we won’t be able to tell whether it’s prime or composite. We can’t even tell, without the very last digit, whether the number is odd or even!
. Since that’s a higher power of 10 than the number of decimal places it showed me, I’m concerned that we won’t be able to tell whether it’s prime or composite. We can’t even tell, without the very last digit, whether the number is odd or even! To get a step closer to predicting what happens when n=100, we can try out even more values of n. When doing similar calculations repeatedly, we can save time by using a spreadsheet to organize our work and do the calculations for us just like a handheld calculator could.
So basically, our steps, which you could use in investigating other formulas, were:
- Label columns for input and output
- Set up a version of the formula pointed at the input column in the output column
- Let autofill do its one job
- Examine the results (possibly using the spreadsheet to do some more calculations in the process)
By doing so, we found out that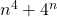 
is neither prime nor composite when n=0, prime when n=1, and composite when n=2 or any greater number we successfully checked. Based on these results, we could very reasonably suspect that “other than the trivial cases n=0 and n=1, the formula evaluates to a composite number.”
is neither prime nor composite when n=0, prime when n=1, and composite when n=2 or any greater number we successfully checked. Based on these results, we could very reasonably suspect that “other than the trivial cases n=0 and n=1, the formula 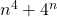evaluates to a composite number.” If that conjecture is true, then we could be sure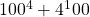 
is composite. However, we only checked our conjecture up to n=#, and being lazy like a mathematician means making sure the shortcuts we use are truly reliable.
is composite. However, we only checked our conjecture up to n=#, and being lazy like a mathematician means making sure the shortcuts we use are truly reliable. So, how do we make sure the output of this formula will be some composite number, without checking the results by hand (which would defeat the purpose of using our conjecture as a shortcut)? We’ll need to find a proof using features of the formula. There are a few options for how to go about that, so this is where I’m going to leave off for now and give you a chance to try things.
By the way, as you examine the formula’s outputs as far as we’ve been able to calculate them so far, you might notice other patterns. Jot down anything you notice and see if you can find a reason why it has to keep working, and if you want, use it to make predictions about the formula’s behavior for difficult-to-calculate values of n.
Calc You Later!
Leave a Reply
You must be logged in to post a comment.