Hello mathematicians, puzzlers, and other curious people!
In the previous step of this investigation, we arrived at a conjecture that “other than the trivial cases n=0 and n=1, the formula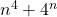 
evaluates to a composite number.” If this is true, it gives us an extreme shortcut, compared to working out the actual value after plugging a big number like 100 in for n, but is it actually, reliably, always true?
evaluates to a composite number.” If this is true, it gives us an extreme shortcut, compared to working out the actual value after plugging a big number like 100 in for n, but is it actually, reliably, always true? We can find a clue that helps us prove this claim at least part of the time in our work from the previous step, where we classified numbers generated by this formula as either prime or composite. If you don’t remember how we did that, it could be a good idea to refresh your memory.
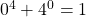is neither prime nor composite
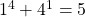is prime
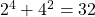is composite
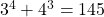is composite
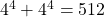is composite
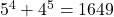is composite
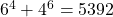is composite- …and so on — the rest we tried were composite.
We very quickly noticed that the formula’s output was even and therefore composite when n was any of the even numbers that we tried as inputs. Since 100, which we’ve been using as an example value of n, is even, being able to tell that this pattern will hold would give us an answer to the particular question of whether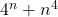 
is prime or composite. So, let’s try for a moment considering the even case by supposing n=2k. (If this works, we could later suppose 
, the odd case, and combine the two into a proof that covers all values of n.)
is prime or composite. So, let’s try for a moment considering the even case by supposing n=2k. (If this works, we could later suppose 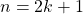, the odd case, and combine the two into a proof that covers all values of n.) We’ll proceed by plugging in 2k, giving us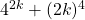 
, and attempting to rewrite that expression in a way that shows it has factors.
, and attempting to rewrite that expression in a way that shows it has factors. Since we can see from this that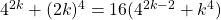 
, we can conclude that 16 and 
is a factor pair for , which is when n is even. So, when n is even, we can be sure that will be composite, because we can calculate a factor pair other than itself and 1. In particular, for our 
example, this number will be composite with one factor pair being 16 and 
(which would still be tricky to completely evaluate, but we know it’s a number that exists).
, we can conclude that 16 and 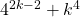is a factor pair for 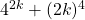, which is 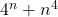when n is even. So, when n is even, we can be sure that 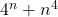will be composite, because we can calculate a factor pair other than itself and 1. In particular, for our 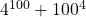example, this number will be composite with one factor pair being 16 and 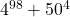(which would still be tricky to completely evaluate, but we know it’s a number that exists). We can now we sure that “other than the trivial case n=0, whenever n is even, the formula 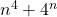evaluates to a composite number,” so this statement is no longer a conjecture — you could call it a theorem, lemma, proposition etc., depending on how you plan to organize your work on the topic. But, what we wanted to say is “other than the trivial cases n=0 and n=1, the formula evaluates to a composite number.” (What if, for example, n=99? That would be almost equally difficult to calculate as when n=100.)
evaluates to a composite number,” so this statement is no longer a conjecture — you could call it a theorem, lemma, proposition etc., depending on how you plan to organize your work on the topic. But, what we wanted to say is “other than the trivial cases n=0 and n=1, the formula 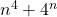evaluates to a composite number.” (What if, for example, n=99? That would be almost equally difficult to calculate as when n=100.) See what you can come up with, and in the next article I’ll take a look at the factorization suggested by the article.
Calc You Later!
Leave a Reply
You must be logged in to post a comment.