Happy e-Day of the Century!

What is $e$ -Day?

Well, what is $e$ ?

We know $e$ as the mysterious number that shows up in the compound interest formula $A=Pe^{rt}$ and its close relative the compound growth and decay formula $A=A_0e^{kt}$ , but what is $e$ really?

We say that $e \\approx 2.718$ or $e = 2.71828182845904523536...$ , but the choice between $\\approx$ and … renders these ways of talking about $e$ unsatisfactory to mathematicians (though they might be quite all right for engineers and other solvers of application problems). The first of these approximations, 2.718, however, reveals the importance of today: in the month-first date writing system favored in the United States, today is 2-7-18, a four-digit approximation of $e$ . While 2-7 comes around every year, that approximation differs from $e$ by 0.018281828…, or about $\\frac{1}{149}$ of $e$ , which sounds like a small amount but could accumulate to a problematic amount of error across a large calculation. Today\’s date, 2-7-18, on the other hand, which comes around once per century, approximates $e$ to within about $\\frac{1}{9645}$ of $e$ , more than 64 times as accurate as the annual two-digit approximation.

Apologies, of course, to those who put the day before the month; your $e$ -day isn\’t until July 2nd (but you got Palindrome Day this year before us).

All these approximations raise the question of how they might be calculated. As you might remember from strategies you used problem-solving on interest problems with decreasing compounding periods, the limit $\\lim_{n \\to \\infty} (1 + \\frac{1}{n})^n$ , where $n$ is the number of compounding periods per year, is exactly equal to $e$ . This limit, however, inconveniently* involves infinity; also, though a limit (provided it exists in the first place) is a number, this expression doesn\’t feel like a specific number in the same way as 4 or -12 or even $\\frac{5}{7}$ . For these reasons we tend to use approximations, like those above, based on \”sufficiently large\” values of $n$ .

*inconvenient, that is, for purposes involving human comprehension

Because of the importance of $e$ as an exponential base, special attention has been paid to the function $f(x)=e^x$ . As a result, mathematicians have determined that this function is perfectly approximated by a Taylor polynomial:

$e^x = \\sum_{n=0}^{\\infty} \\frac{x^n}{n!} \$

This is very important because the infinite number of digits of $e$ makes it difficult (in fact, impossible) to multiply by itself repeatedly the usual way without introducing rounding errors. The Taylor polynomial allows us to calculate powers of $e$ , when they come up in problems, to any level of accuracy we need, with a good deal less trouble.

We know that this function is part of growth and decay functions, so it is natural to examine how this function changes by taking its derivative, and its polynomial version will be especially nice to take a derivative of because that\’s how polynomials are. I\’m starting by writing out the first six terms, but remember, any further terms would follow the same pattern.

$e^x=1+\\frac{x^1}{1!}+\\frac{x^2}{2!}+\\frac{x^3}{3!}+\\frac{x^4}{4!}+\\frac{x^5}{5!}+...$

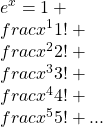
Then we take the derivative, going term-by-term and using the power rule and other basic calculus properties:

$[e^x]\'=1\'+(\\frac{x}{1!})\'+(\\frac{x^2}{2!})\'+(\\frac{x^3}{3!})\'+(\\frac{x^4}{4!})\'+(\\frac{x^5}{5!})\'+...$

$=0+1*\\frac{x^0}{1!}+2*\\frac{x^1}{2!}+3*\\frac{x^2}{3!}+4*\\frac{x^3}{4!}+5*\\frac{x^4}{5!}+...$

$=0+1*\\frac{x^0}{1!}+2*\\frac{x^1}{2*1!}+3*\\frac{x^2}{3*2!}+4*\\frac{x^3}{4*3!}+5*\\frac{x^4}{5*4!}+...$

$=0+x^0+\\frac{x^1}{1!}+\\frac{x^2}{2!}+\\frac{x^3}{3!}+\\frac{x^4}{4!}+...$

$=1+\\frac{x^1}{1!}+\\frac{x^2}{2!}+\\frac{x^3}{3!}+\\frac{x^4}{4!}+...$

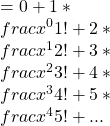
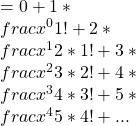
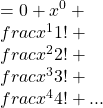
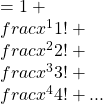
Note that this is precisely the first five terms of the same series, and with the same indication that the pattern continues. So, we have found a remarkable fact: $(e^x)\'=e^x$ .

Given this function\’s extremely close relationship with change, then — up to the point where it represents its own rate of change — we could say that $e$ -Day is a holiday for mathematicians, puzzlers, and other curious people to take some time to think and talk about change, in the world and in their own lives.

What changes would you like to talk about?

Math With Avrila

Happy e-Day of the Century!

— by

Leave a Reply Cancel reply